Question

The standard form for a parabola with vertex (h,k) and an axis of symmetry of y=k is:(y-k)^2=4p(x-h)The graph below is for a parabola. Write it in standard form. When answering the questions type coordinates with parentheses and separated by a comma like this (x,y). If a value is a non-integer then type is a decimal rounded to the nearest hundredth.parabola opening to the right, axis of symmetry at y=2, vertex (-2,2) focus (-31/16,2)The value for p is: AnswerThe value for h is: AnswerThe value for k is: Answer

Answer 1

In the equation of the parabola, the value for p represents the distance between the vertex and the focus. To find it, use the formula to find the distance between 2 points:

`\begin{gathered} d=√((y2-y1)^2+(x2-x1)^2) \\ d=\sqrt{(2-2)^2+(-(31)/(16)-(-2))^2} \\ d=\sqrt{(-(31)/(16)+2)^2} \\ d=\sqrt{((1)/(16))^2} \\ d=(1)/(16) \end{gathered}`

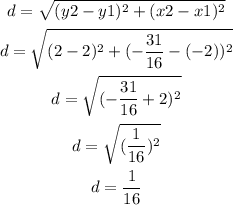
It means that the value of p is 1/16, in decimal form, 0.0625.

The value of h is the x coordinate of the vertex, which is -2.

The value of k is the y coordinate of the vertex, which is 2.