Question

6. The diagram of the wooden block drawn below (not drawn to scale) consists of a cuboid with a small cylinder bored through the centre. 22 Take it = 12 cm 21 cm 14 cm (a) Given that the diameter of the small cylinder is 7 cm, draw a cross-sectional view of the wooden block, showing the measurements of the radius of the circle and the sides of the rectangle. 121 (b) Show that the capacity of the small cylinder is 808.5 cm3. 12] (c) Determine the volume of the material used to make the wooden block 131 (d) Given that the density of the wood used to make the wooden block is 1.6 gcm-3. 121 determine the mass, in kg, of the wooden block. mass (Recall: density = volume

Answer 1

`\begin{gathered} b)True \\ c)3528cm³ \\ d)_0.0016kg \end{gathered}`

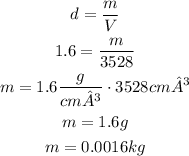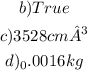
b) By capacity, the problem asks the volume. So let's find the volume of that small cylinder

`\begin{gathered} V=\pi r^2h \\ 808.5=(22)/(7)\cdot((7)/(2))²\cdot21 \\ 808.5=(22)/(7)\cdot(49)/(4)\cdot\:21 \\ 808.5=(1617)/(2) \\ 808.5=808.5 \end{gathered}`

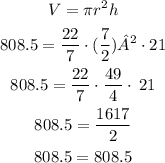
So by plugging into the formula the given data we can tell that the capacity of that cylinder is indeed 808.5cm³

c) Note that now, the point is to find the Volume of that cuboid (rectangular prism), which we can find by doing the following formula:

`\begin{gathered} V=A_b\cdot h \\ V=(14\cdot12)\cdot21 \\ V=3528cm³ \end{gathered}`

d) And finally, the density is given by the following ratio:

`\begin{gathered} d=(m)/(V) \\ 1.6=(m)/(3528) \\ m=1.6(g)/(cm³)\cdot3528cm³ \\ m=1.6g \\ m=0.0016kg \end{gathered}`