Question

2. The area of the side surface of a regular quadrilateral pyramid is 14.76 cm2 and the total surface area is 18 cm2.Calculate the pyramid's altitude H and volume V.

Answer 1

Given:

Area of side surface of rectangular pyramid = 14.76 cm²

Total surface area = 18 cm²

Let's find the pyramid's altitude and the volume of the pyramid.

To find the altitude, H, let's first find the slant height.

`A_s=(1)/(2)*p*s`

Where:

p is the perimeter of the base

s is the slant height

As is the area of the side surface.

• To find the perimeter of the base, let's find the base area.

Base area = Total surface area - Area of side surface.

Base area = 18 cm² - 14.76 cm² = 3.24 cm²

• Let's find the length of one side of the base:

`\begin{gathered} l=√(3.24) \\ \\ l=1.8\text{ cm} \end{gathered}`

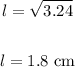
The length of one side of the base is 1.8 cm.

• To find the perimeter, apply the formula:

`\begin{gathered} p=l*4 \\ \\ p=1.8*4 \\ \\ p=7.2\text{ cm} \end{gathered}`

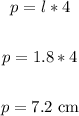
Let's plug in 7.2 cm for p, 14.76 for As and solve for the slant height s:

`\begin{gathered} A_s=(1)/(2)*p*s \\ \\ 14.76=(1)/(2)*7.2*s \\ \\ 14.76=3.6s \\ \\ s=(14.76)/(3.6) \\ \\ s=4.1\text{ cm} \end{gathered}`

The slant height is 4.1 cm.

To find the altitude, H, apply Pythagorean theorem:

`\begin{gathered} H=\sqrt{4.1^2-((1.8)/(2))^2} \\ \\ H=√(16.81-0.81) \\ \\ H=\text{4 cm} \end{gathered}`

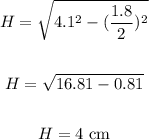
The pyramid's altitude, H = 4 cm.

To find the volume, apply the formula:

`V=(1)/(3)*b*H`

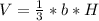
Where:

b is the base area = 1.8 x 1.8 = 3.24 cm²

H is the altitude = 4 cm

Thus, we have:

`\begin{gathered} V=(1)/(3)*3.24*4 \\ \\ V=4.32\text{ cm}^3 \end{gathered}`

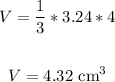
The volume is 4.32 cm³.

ANSWER:

• H = 4 cm

,

• V = 4.32 cm³