Question

A rope has length 3.72 m, cross sectional area of 0.154 x 10-4 m^2, and Young's modulusof 19.1 x10^10 N•m^-2. A load of mass 286 kg hangs from the rope.A) What is the increase in length (in mm) of the rope?

Answer 1

Given data:

* The original length of the rope is L = 3.72 m.

* The area of cross-section of rope is,

`A=0.154*10^(-4)m^2`

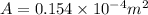
* The Young's modulus of rope is,

`Y=19.1*10^(10)Nm^(-2)`

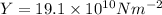
* The mass of the load is,

`m=286\text{ kg}`

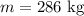
Solution:

The weight of the load is,

`\begin{gathered} W=mg \\ W=286*9.8 \\ W=2802.8\text{ N} \end{gathered}`

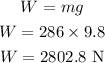
Young's modulus of the rope in terms of the weight, area, and the original length of the rope is,

`Y=(WL)/(Al)`

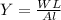
where l is the change in the length,

Substituting the known values,

`\begin{gathered} 19.1*10^(10)=(2802.8*3.72)/(0.154*10^(-4)* l) \\ l=(2802.8*3.72)/(0.154*10^(-4)*19.1*10^(10)) \end{gathered}`

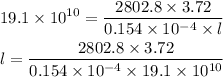
By simplifying,

`\begin{gathered} l=(10426.416)/(2.9414*10^6) \\ l=3544.7*10^(-6)\text{ m} \\ l=3.54*10^(-3)\text{ m} \\ l=3.54\text{ mm} \end{gathered}`

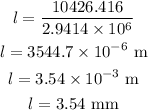
Thus, the increase in the length of the rope is 3.54 mm.