Question

Suppose that the functions s and t are defined for all real numbers x as follows. s(x) = 4x - 1 t(x) = x + 1Write the expressions for (st)(x) and (s + t)(x) and evaluate (s - t)(4)

Answer 1

(s·t)(x) = 4x² + 3x - 1

(s + t)(x) = 5x

(s - t)(4) = 10

Step-by-step explanation:

We know that

s(x) = 4x - 1

t(x) = x + 1

Then, we can calculate (s·t)(x), (s + t)(x), and (s - t)(x) ad follows

`\begin{gathered} (s\cdot t)(x)=s(t)\cdot t(x) \\ (s\cdot t)(x)=(4x-1)(x+1) \\ (s\cdot t)(x)=4x(x)+4x(1)-1(x)-1(1) \\ (s\cdot t)(x)=4x^2+4x-x-1 \\ (s\cdot t)(x)=4x^2+3x-1 \end{gathered}`
`\begin{gathered} (s+t)(x)=s(t)+t(x) \\ (s+t)(x)=(4x-1)+(x+1) \\ (s+t)(x)=4x-1+x+1 \\ (s+t)(x)=5x \end{gathered}`
`\begin{gathered} (s-t)(x)=s(x)-t(x) \\ (s-t)(x)=(4x-1)-(x+1) \\ (s-t)(x)=4x-1-x-1 \\ (s-t)(x)=3x-2 \end{gathered}`

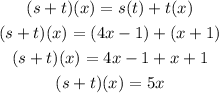
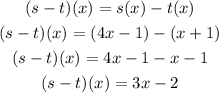
Finally, we can calculate (s-t)(4) replacing x by 4 on the equation (s - t)(x), so

`\begin{gathered} (s-t)(4)=3(4)-2 \\ (s-t)(4)=12-2 \\ (s-t)(4)=10 \end{gathered}`

Therefore, the answers are

(s·t)(x) = 4x² + 3x - 1

(s + t)(x) = 5x

(s - t)(4) = 10