Question

Line segment XY begins at ( - 6,4) and ends at ( - 2,4). The segment is reflected over the x-axis and translated left 3 units to form line segment X ‘ Y ‘. Enter the length , in units , of the lines segment X’ Y’ .

Answer 1

4 units

Step-by-step explanation

The transformations made to the line segment XY are a reflection and a translation. Both of these transformations do not change the size of the figure, so the length of line segment X'Y' is the same as the length of line segment XY.

The distance between two points (x₁, y₁) and (x₂, y₂) is found with the Pythagorean Theorem,

In this case, the endpoints of line segment XY are (-6, 4) and (-2, 4), so its length is,

`d=√((-6-(-2))^2+(4-4)^2)=√((-6+2)^2+0^2)=√((-4)^2)=√(16)=4`

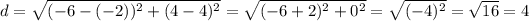
Hence, the length of line segment X'Y' is 4 units.