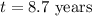Answer:
a) the amount of time in years it will take for the given investment to double is;
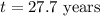
b) the amount of time in years it will take for the given investment to double is;
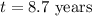
Step-by-step explanation:
Given that under continuous compounding, the amount of time t in years required for an investment to double is a function of the interest rate r according to the formula;
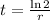
a) we want to find the amount of time it will take a $3000 investment to reach $6000 (i.e double) for an interest rate of 2.5%.
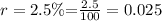
Applying the given formula;
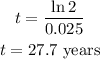
Therefore, the amount of time in years it will take for the given investment to double is;
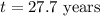
b) we want to find the amount of time it will take a $3000 investment to reach $6000 (i.e double) for an interest rate of 8%.
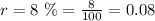
Applying the given formula;
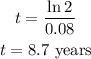
Therefore, the amount of time in years it will take for the given investment to double is;