Question

Triangle ABC is shown:What statement must be true?cos(A) = sin(A)cos(A) = sin(B)cos(A) = cos(B)sin(A) = sin(B)

Answer 1

The statement that must be true is;

`\cos \text{ A = sin B}`

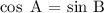
Here, we want to select the correct option

The triangle we can see is a right-angled triangle

That means the two angles are complementary

When two angles are complementary, they add up to be 90

Thus, we have it that;

`A\text{ + B = 90}`

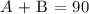
Now, let us consider the options.

a) The sine of an angle is not the same value as its cos, except if the angle is 45 degrees. Since we cannot ascertain that the angles are 45 degrees in value, then the statement must not be true

b) cos A = sin B

This is possible

This is because, the sine of an angle is equal to the cosine of its complement and also; the cosine of an angle is equal to the sine of its complement

We have this as;

`\begin{gathered} A\text{ + B = 90} \\ A\text{ = 90-B} \\ \sin \text{ A = cos (90-A)} \\ 90-A\text{ = B} \\ \sin \text{ A = cos B} \end{gathered}`

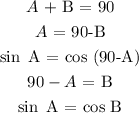
The last two cases are only true if A = B which means the angle is 45. Since we cannot confirm this, then we can say that only the second statement is a possibility