Question

Jennifer hits a stationary 0.20-kg ball, and it leaves her racket at 40 m/s. Time-lapse photography shows that the ball was in contact with the racket for 40 ms.What average force did the ball exert on the racket?Express your answer using two significant figures.What is the ratio of this force to the weight of the ball?Express your answer using two significant figures.

Answer 1

Given:

The mass of the stationary ball is: m = 0.20 kg.

The velocity of the ball when it leaves the rocket is: Vf = 40 m/s.

The time for which the ball was in contact with the rocket is: t = 40 ms = 0.04 s.

To find:

The average force the ball exerts on the rocket.

The ratio of the force on a rocket to the weight of the ball.

Step-by-step explanation

As the ball is initially stationary, its initial velocity Vi is zero. After the ball was hit, it moves with the velocity Vf = 40 m/s for time t = 0.04 s.

Thus, using Newton's second law, we get:

`\begin{gathered} F=ma \\ \\ F=m*(V_f-V_i)/(t) \end{gathered}`

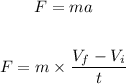
Substituting the values in the above equation, we get:

`\begin{gathered} F=0.20\text{ kg}*\frac{40\text{ m/s}-0\text{ m/s}}{0.04\text{ s}} \\ \\ F=200\text{ kg.}^\text{m/s}^2 \\ \\ F=200\text{ N} \end{gathered}`

The weight of the ball on the earth is the product of its mass and acceleration due to gravity g. The value of the acceleration due to earth is: g = 9.8 m/s^2.

The weight W of the ball on earth is given as:

`W=mg`

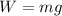
Substituting the values in the above equation, we get:

`\begin{gathered} W=0.20\text{ kg}*9.8\text{ m/s}^2 \\ \\ W=1.96\text{ N} \end{gathered}`

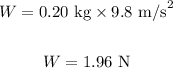
The ratio of the force F exerted by the ball on the rocket and the weight of the ball is:

`\begin{gathered} (F)/(W)=\frac{200\text{ N}}{1.96\text{ N}} \\ \\ (F)/(W)=(102.04)/(1) \end{gathered}`

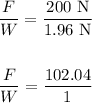
Thus, F : W = 102.04 : 1.

Final answer:

The force exerted by the ball on the rocket is 200 N. The ratio of this force and the weight of the ball is 102.04 : 1.