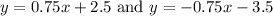24)
Given:
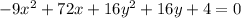
We need to find the hyperbola in standard form
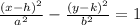
The given equation can be written as follows.
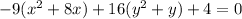
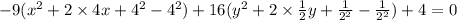
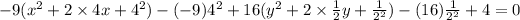
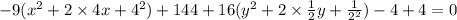
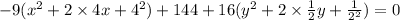
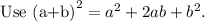

Subtracting 144 from both sides, we get
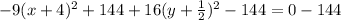
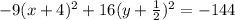
Dividing both sides by (-144), we get
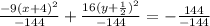


Hence we get the standard form of the hyperbola.
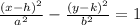
Comapring with standerd form, we get
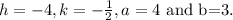
The coordinates of the vertices are
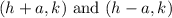
Substitute h=-4, a=4 and k=-1/2.

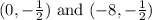
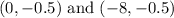
Hence the vertices are (0, -0.5) and (-8, -0.5).
The distance between foci is 2c,
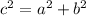
Substitute a=4 and b=3 to find the value of c.
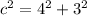

![c=\pm\sqrt[]{25}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/xr05vrmhsn9f20my0wyj.png)

The measure of distance can not be negative.
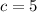
The coordinates of the foci are
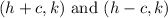
Substitute h=-4, k=-1/2 and c=5, we get
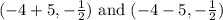

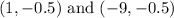
Hence the foci are
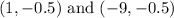
The equation of the asymptotes are
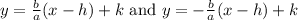
Substitute a=4,b=3,h=-4 and k=-1/2, we get
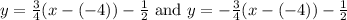
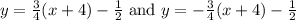
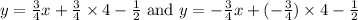
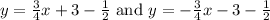
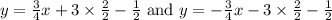
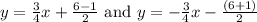
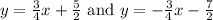
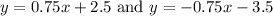
Hence the equations of the asymptotes are
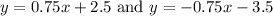
Results:
The equation for the hyperbola in standard form is

The vertices are
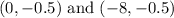
The foci are
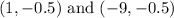
The equation of asymptotes are