Question

1. Consider the folowing diagram. B Part A: Which of the following statements is enough to prove that ABCD is a kite but not any other quadrilateral? A ABCD has at least one pair of congruent opposite angles. B Not all four sides of ABCD are equal, but there are two palrs of equal adjacent sides. C The diagonals of ABCD are perpendicular to each other. D The diagonals of ABCD form four right triangles. Part B: Complete the following statement. If ABCD is a kite, EB is 24 meters long, EC is 10 meters long, and EA is 80 meters long, the perimeter of ABCD measures meters and the area of ABCD measures square meters.

Answer 1

A kite is a quadilateral where two disjoint pairs of sides are equal. A kite has two pairs of equal sides that are adjacent to each other.

In a kite, all four sides are not equal.

For the quadilateral given ABCD to be cosidered a kite, the correct statement that is enough to prove this is:

Not all four sides of ABCD are equal, but there are two palrs of equal adjacent sides.

Given:

EB = 24 meters

EC = 10 meters

EA = 80 meters

To find the perimeter of the kite, first find AB and BC.

To find AB use pythagoras theorem since ABE forms a right triangle.

We have:

`\begin{gathered} AB^2=EA^2+EB^2 \\ \\ AB^2=80^2+24^2 \\ \\ AB^2=6400+576 \\ \\ AB^2=6976 \\ \\ AB=\sqrt[]{6976} \\ \\ AB=83.5\text{ meters} \end{gathered}`

Let's also Find BC using pythagoras theorem:

`\begin{gathered} BC^2=EC^2+EB^2 \\ \\ BC^2=10^2+24^2 \\ \\ BC^2=100+576 \\ \\ BC^2=676 \\ \\ BC=\sqrt[]{676} \\ \\ BC=26\text{ meters} \end{gathered}`

Therefore, to find the perimeter of the kite use the formula:

P = 2(AB + BC)

P = 2(83.5 + 26)

P = 219 meters

To find the area, use the formula below:

`A=(AC\ast BD)/(2)`

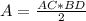
Where

AC= 80 + 10 = 90 meters

BD = 24 + 24 = 48

`A=(90\ast48)/(2)=(4320)/(2)=2160m^2`

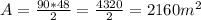
ANSWER:

B. Not all four sides of ABCD are equal, but there are two palrs of equal adjacent sides.

Perimeter = 219 meters

Area = 2160 meters square