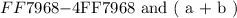Question

The factors of the expression -4 * a + b r -4 +

Answer 1

We are to determine the factors of the given expression as follows:

`-4\cdot(\text{ a + b ) }`

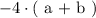
A factor can be an integer or an expression that is perfectly divisible by dividend. In this case:

`-4a\text{ - 4b }\ldots\text{ Dividend}`

We can make factors of the above expression on the basis of divisibility of the entire expression. Since the values of ( a ) and ( b ) are dissimilar the expression has no divisibility of either of these. Hence, the only common factor of the expression is the integer ( 4 ).

We multiply and divide the entire expression by ( -4 ) as follows:

`\begin{gathered} (-4)/(-4)\cdot\text{ ( -4a - 4b ) = -4 }\cdot\text{ ( }\frac{-4a\text{ - 4b}}{-4}) \\ \\ \textcolor{#FF7968}{-4\cdot}\text{\textcolor{#FF7968}{ ( a + b ) }} \end{gathered}`

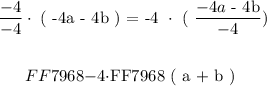
After the operation of divisibility we get two things. One: Quotient, Two: Remainder. The factors are then expressed as:

`\text{\textcolor{#FF7968}{Factors:}}\text{ Quotient x Remainder}`

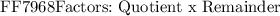
The product of two factors expresses the entire expression. Hence, the two factors are:

`\textcolor{#FF7968}{-4}\text{\textcolor{#FF7968}{ and ( a + b )}}`