Question

For a social studies project, Darius has to make a map of a neighborhood that could exist in his hometown. He wants to make a park in the shape of a right triangle. He has already planned 2 of the streets that make up 2 sides of his park. The hypotenuse of the park is 3rd Avenue, which goes through points (-3, 2) and (9, 7) on his map. One of the legs is Elm Street, which goes through (12, 5) and has a slope of -23. The other leg of the park will be Spring Parkway and will go through (-3, 2) and intersect Elm Street.A) What is the slope of Spring Parkway?B) What is the length, in units, of 3rd Avenue?C) The variable x represents the length of Spring Parkway in units. The measure of the angle formed by Spring Parkway and 3rd Avenue is approximately 33.69°. Write a trigonometric equation relating the measure of the angle formed by Spring Parkway and 3rd Avenue, the length of Spring Parkway (x), and the length of 3rd Avenue from part B.D) Solve for x, the length of Spring Parkway in units.

Answer 1

A) Slope = 1/5

B) Length = 13 units

(C) Equation: x = 13cos33.69°

(D) X = 10.82 units

Step-by-step explanation

The given information in the question is represented in the figure below:

Step-by-step solution:

(A) The slope of Spring Parkway.

This can be calculated using the slope in two points formula

`slope=(y_2-y_1)/(x_2-x_1)=(5-2)/(12--3)=(3)/(12+3)=(3)/(15)=(1)/(5)`

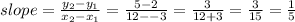
Slope = 1/5

(B) The length, in units, of 3rd Avenue.

The length, in units of 3rd Avenue, can be determined using distance between two points as follows

`\begin{gathered} L=√((x_2-x_1)^2+(y_2-y_1)^2) \\ \\ L=√((9-(-3)^2+(7-2)^2) \\ \\ L=√((9+3)^2+5^2) \\ \\ L=√(12^2+5^2) \\ \\ L=√(144+25) \\ \\ L=√(169) \\ \\ L=13\text{ }units \end{gathered}`

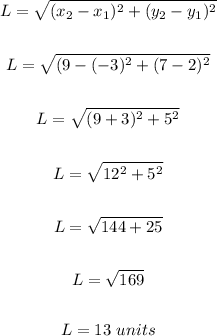
Length = 13 units

(C) Since variable x represents the length of Spring Parkway in units and the measure of the angle formed by Spring Parkway and 3rd Avenue is approximately 33.69°, then the trigonometric equation relating the measure of the angle formed by Spring Parkway and 3rd Avenue, the length of Spring Parkway (x), and the length of 3rd Avenue from part B will be

`\begin{gathered} cos\text{ }\theta=(Adjacent)/(Hypotenuse) \\ \\ \theta=33.69°,Adjacent=x,and\text{ }Hypotenuse=13\text{ }units \\ \\ \therefore cos\text{ }33.69°=(x)/(13) \\ \\ x=13cos\text{ }33.69° \end{gathered}`

Equation: x = 13cos33.69°

(D) To solve for x, the length of Spring Parkway in units, use the trigonometric equation in part C above.

`\begin{gathered} x=13cos33.69 \\ \\ x=13*0.8321 \\ \\ x=10.82\text{ }units \end{gathered}`

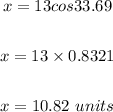
X = 10.82 units.