Step-by-step explanation
From the statement, we have a normal distribution for the life expectancy of tires with:
• variable X = life expectancy in miles,
,
• mean μ = 40,000 ml,
,
• standard deviation σ = 2,000 ml.
A) We must compute the probability:
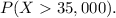
We calculate the z-score for this probability:
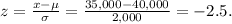
Using a table for z-scores, we find that:

So a tire selected at random has a 99.379% probability of having a tread life of more than 35,000 miles.
B) Now, if four new tires are installed in a car, we want to know the probability that all four tires are still useful tread after 35,000 of driving.
From question A, we know that each wire has a probability of Pₐ = 0.99373 of having a tread life of more than 35,000 miles. We assume that the tread lives of the tires are independent of each other. So the total probability that the four wires will be useful after 35,000 of driving is:
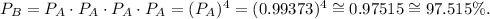
Answer
A) 99.379%
B) 97.515%