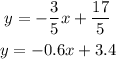Question

Find the equation of a line parallel to -3x - 5y = -6 that contains the point (-4,1). Write the equation in slope-intercept form.

Answer 1

y=-0.6x+3.4

Explanation:

First, by definition, two lines are parallel if they have the same slope.

Given the equation of the line:

`-3x-5y=-6`

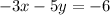
We find the slope by rewriting the line in the slope-intercept form:

`y=mx+b\text{ where }\begin{cases}m={Slope} \\ b={y-intercept}\end{cases}`

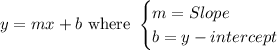
This gives:

`\begin{gathered} -3x+6=5y \\ y=-(3x)/(5)+(6)/(5) \\ \implies\text{ The slope}=-(3)/(5) \end{gathered}`

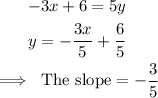
Since the two lines are to be parallel, the new line will have a slope of -3/5 and pass through the point (-4,1).

Substitute x=-4, y=1 and m=-3/5 into the slope-intercept form:

`\begin{gathered} y=mx+b \\ 1=-4((3)/(5))+b \\ b=1+(12)/(5) \\ b=3.4 \end{gathered}`

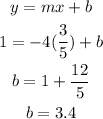
The equation of the line is:

`\begin{gathered} y=-(3)/(5)x+(17)/(5) \\ y=-0.6x+3.4 \end{gathered}`