Comparing with a cubic function with the same leading coefficient, we have it that the graphs of both functions are similar as they have excatly the same end behavior summarised below;
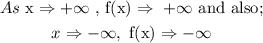
Here, we want to make a comparism
Before we go on to make the comparism, we want to describe the graph
As can be seen from the given equation of the graph, we have a positive leading coefficenit (the coefficeint of the highest power; x^5 in this case) and an odd degree (degree refers to the highest power of the polynomial)
Using this, we can get the property of the the graph
The property is simply that;

Now, for a cubic function with the same leading coefficient (+1 which is positive) and the degree which is 3; both functions have the same end properties