Question

Ex 3.7
12. find the area between the curve y=x³-2 and the y-axis between y= -1 and y=25

Answer 1

Yeah, you'd have to use the inverse function to produce this result.

Let's get the inverse function first:


`y={ x }^( 3 )-2\\ \\ { x }^( 3 )=y+2\\ \\ x=\sqrt [ 3 ]{ y+2 }`


`\\ \\ \therefore \quad { f }^( -1 )\left( x \right) =\sqrt [ 3 ]{ x+2 }`

Now, we can solve the problem using:


`\int _( -1 )^( 25 ){ \sqrt [ 3 ]{ x+2 } } dx`

But to solve the problem more easily we make u=x+2, therefore du/dx=1, therefore du=dx.

When x=25, u=27.

When x=-1, u=1.

Now:


`\int _( 1 )^( 27 ){ { u }^{ \frac { 1 }{ 3 } } } du\\ \\ ={ \left[ \frac { 3 }{ 4 } { u }^{ \frac { 4 }{ 3 } } \right] }_( 1 )^( 27 )`


`\\ \\ =\frac { 3 }{ 4 } \cdot { 27 }^{ \frac { 4 }{ 3 } }-\frac { 3 }{ 4 } \cdot { 1 }^{ \frac { 4 }{ 3 } }\\ \\ =\frac { 3 }{ 4 } { \left( { 3 }^( 3 ) \right) }^{ \frac { 4 }{ 3 } }-\frac { 3 }{ 4 }`


`\\ \\ =\frac { 3 }{ 4 } \cdot { 3 }^( 4 )-\frac { 3 }{ 4 } \\ \\ =\frac { 3 }{ 4 } \left( { 3 }^( 4 )-1 \right)`


`\\ \\ =\frac { 3 }{ 4 } \cdot 80\\ \\ =60`

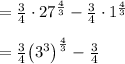
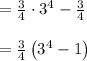
Answer: 60 units squared.

Answer 2

`y=x^3-2\\ x^3=y+2\\ x=\sqrt[3]{y+2}\\\\ \int \limits_(-1)^(25)\sqrt[3]{y+2}\, dy=\\ \int \limits_(-1)^(25)(y+2)^{\tfrac{1}{3}}\, dy=\\ \left[\frac{(y+2)^{\tfrac{4}{3}}}{(4)/(3)} \right]_(-1)^(25)=\\`

`\left[(3)/(4)(y+2)^{\tfrac{4}{3}} \right]_(-1)^(25)=\\ \left[(3)/(4)(y+2)\sqrt[3]{y+2} \right]_(-1)^(25)=\\ (3)/(4)(25+2)\sqrt[3]{25+2}-\left((3)/(4)(-1+2)\sqrt[3]{-1+2}\right)=\\ (3)/(4)\cdot27\sqrt[3]{27}-\left((3)/(4)\sqrt[3]{1}\right)=\\ (3)/(4)\cdot27\cdot3-(3)/(4)=\\ (3)/(4)(81-1)=\\ (3)/(4)\cdot 80=\\3\cdot20=\\ 60`