Question

The rectangle has an area of 144 square centimeters. which is the perimeter?

Answer 1

The formula to find the area of a rectangle is:

`\begin{gathered} A=L\cdot W \\ \text{ Where} \\ A\text{ is the area} \\ L\text{ is the length} \\ W\text{ is the width} \end{gathered}`

Then, let it be:

• L: The length of the rectangle.

,

• W: The width of the rectangle.

So, we have:

`\begin{gathered} A=144cm^2 \\ L=? \\ W=8cm \end{gathered}`

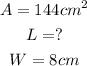
Now, we can write and solve for L the following equation:

`\begin{gathered} A=L\cdot W \\ 144cm^2=L\cdot8cm \\ \text{ Divide by 8}cm\text{ from both sides} \\ (144cm^2)/(8cm)=(L\cdot8cm)/(8cm) \\ 18cm=L \end{gathered}`

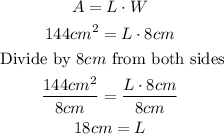
The following is the procedure for dividing 144 by 8.

On the other hand, the perimeter is the sum of the measures of all sides of a polygon. Then, we have:

`\begin{gathered} \text{Perimter}=L+W+L+W \\ \text{Perimter}=18cm+8cm+18cm+8cm \\ \text{Perimter}=52cm \end{gathered}`

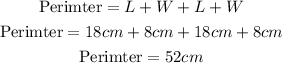
Therefore, the perimeter of the rectangle is 52 cm.