Question

A sugar cube of mass m was placed at the top of this inclined plane. It is released from rest, and slides all the way down. The coefficient of kinetic friction between the sugar cube and the inclined plane is µ .What is the sugar cube's kinetic energy at the bottom?

Answer 1

Here to solve this question we can use Work energy theorem.

Work energy theorem:- Work done by all the forces is equal to change in kinetic energy.

`\begin{gathered} W(all\text{ }forces)=\text{ }change\text{ in }K.E.=\Delta K.E. \\ where,\text{ }K.E.=\text{ }Kinetic\text{ }Energy \end{gathered}`

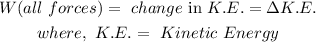
There are only two forces acting on the sugar cube, one is gravitational force and other is friction force.

work done by gravitational force is,

`W(g)=mgh`

And work done by friction is,

`\begin{gathered} W(f)=Force* Displacement\text{ }=-\mu NL \\ here,\text{ minus sign is there because the dirction of frictional force is in the opposite direction of } \\ the\text{ }displacement. \\ \mu=coefficient\text{ }of\text{ }kinetic\text{ }friction \\ N=normal\text{ }reaction\text{ }on\text{ the sugar cube}=mgcos(\theta) \\ \\ \\ \end{gathered}`
`\begin{gathered} So,W(f)=-\mu mgcos(\theta)L \\ \end{gathered}`

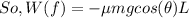
Now applying work energy theorem,

`\begin{gathered} W(g)+W(f)=\Delta K.E.=(K.E.)f-(K.E.)i \\ and\text{ we know that initial kinetic energy of the sugar cube = 0} \\ So,\text{ \lparen}K.E.)i=0 \\ So\text{ our new equation is} \\ W(g)+W(f)=(K.E.)f \\ So,(K.E.)f=W(g)+W(f) \\ (K.E.)f=mgh+(-\mu mLgcos(\theta)0=mgh-\mu mLgcos(\theta) \end{gathered}`

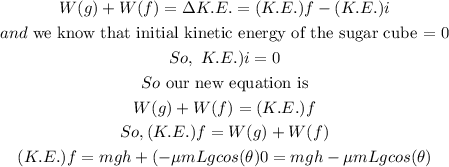
So,

Result :- Option (a) is correct option.