Question

The Agency for Healthcare Research and Quality reported that 53% of people who had coronary bypass surgery in 2008 were over the age of 65. Suppose 15 coronary bypass surgery patients from the year 2008 are chosen. What is the probability that: (Express answers to 4 decimal places) a) exactly 8 of the patients were over the age of 65 when they had their surgery? b) fewer than 10 of the patients were over the age of 65 when they had their surgery? c) between 6 and 11 of the patients were over the age of 65 when they had their surgery? d) more than 12 of the patients were over the age of 65 when they had their surgery? e) would it be unusual that all 15 of the patients were over the age of 65 when they had their surgery?(Remember: "between" does not include the endpoints of an interval of discrete numbers.)

Answer 1

Given:

Percentage of people over 65 = 53%

Sample = 15

Let's solve for the following:

• (a). Exactly 8 of the patients were over the age of 65 when they had their surgery?

Here, we are to apply binomial probability.

We have:

`\begin{gathered} P(x=8)=(^(15)_8)(0.53)^8(1-0.53)^(15-8) \\ \\ P(x=8)=(^(15)_8)(0.53)^8(0.47)^7 \\ \\ p(x=8)=0.2030 \end{gathered}`

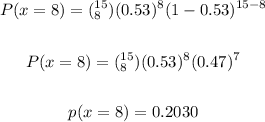
The probability is 0.2030

• (b). Fewer than 10 of the patients were over the age of 65 when they had their surgery?

Here, we are to find P(x < 10).

Using binomial probability, we have:

`\begin{gathered} P(x<10)=P(x=0)+P(x=1)+P(x=2)+P(x=3)......P(x=9) \\ \\ P(x<10)=\sum_{x\mathop{=}0}^9(^(15)_x)(0.53)^x(1-0.53)^(15-x) \\ \\ Using\text{ the calculator, we have:} \\ P(x<10)=0.7875 \end{gathered}`

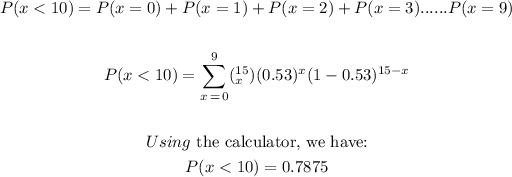
The probability is 0.7875

• (c). Between 6 and 11 of the patients were over the age of 65 when they had their surgery?

Since between does not include the endpoints of the interval, we are to find:

P(6 < x < 11) = P(x = 7) + P(x = 8) + P(x = 9) + P(x = 10)

Hence, we have:

• (e). Would it be unusual that all 15 of the patients were over the age of 65 when they had their surgery?

We are to find P(x = 15):

`\begin{gathered} P(x=15)=(^(15)_(15))(0.53)^(15)(1-0.53)^(15) \\ \\ P(x=15)=(_(15)^(15))(0.53)^(15)(0.47)^(15) \\ \\ P(x=15)=0.0001 \end{gathered}`

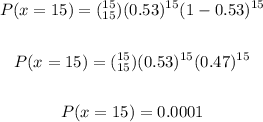
ANSWER:

• (a). 0.2030

,

• (b). 0.7875

,

• (c). 0.6814

,

• (d). 0.0071

,

• (e). 0.0001