Question

For positive acute angles A and B, it is known thatcos A = 28/53 and tan B = 7/24Find the value of cos(A + B) in the simplest form.

Answer 1

We can start solving this problem by using the following property of the cosine of a sum:

`\cos (A+B)=\cos A\cdot\cos B-\sin A\cdot\sin B`

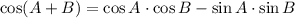
Now, let's notice that the trigonometric relations are obtained by comparing the sides of a right triangle. So, we have:

So, we can find the missing sides a and b, and then use them to calculate sin A, cos B, and sin B.

53² = a² + 28²

a = √(53³-28²)

a = √(2025)

a = 45

and

b² = 24² + 7²

b = √(24² + 7²)

b = √(625)

b = 25

So, we have:

• sin A = a/53 = 45/53

,

• sin B = 7/b = 7/25

,

• cos B = 24/b = 24/25

Now, we can use those values to find: