Question

calculate the value of m if the lines 3x-my=15 makes an angle of 45° with the line 3x+5y=7please help me to solve this?

Answer 1

To find angle between two lines, we use the formula,

`\tan \theta=(m_1-m_2)/(1+m_1m_2)`

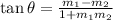
Where

θ is the angle between two lines

m1 is the slope of the first line

m2 is the slope of the second line

First Line Equation:

`\begin{gathered} 3x-my=15 \\ my=3x-15 \\ y=(3)/(m)x-(15)/(m) \end{gathered}`

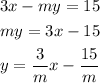
The slope is 3/m

Second Line Equation:

`\begin{gathered} 3x+5y=7 \\ 5y=-3x+7 \\ y=-(3)/(5)x+(7)/(5) \end{gathered}`

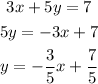
The slope is -3/5

The angle between the two lines is 45°.

Let's substitute the known information into the formula and figure out the value of 'm':