Question

Find the probability that a randomly chosen point is the figure lies in the shaded region. Give all answers in fraction and percent forms. help with #7

Answer 1

In order to determine the probability that a randomly chosen point lies in the shaded region of the figure we just have to divide the area of the shaded region by the total area.

As you can see in figure #7, the shaded area is the region bounded by the box and out of the two circles, then in order to determine the magnitude of the shaded resion we just have to subtract the area of the two circles from the area of the rectangle, like this:

Area of each circle

Each circle has a diameter of 2, then the radius of each circle is 1 (2/2), by replacing the radius r into the following formula, we can calculate the area of each circle:

`\begin{gathered} A=\pi r^2 \\ A=\pi(1)^2 \\ A\approx3.14 \end{gathered}`

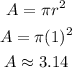
Then the area of each circle is abot 3.14, by multiplying this area by 2 we can determine the total area of the two circles like this:

`At=2*3.14=6.28`

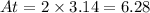
Then the area of the two circles is 6.28.

The area of the rectangle can be calculated by multiplying the width and the length of the rectangle, to get:

`Ar=4*3=12`

Then, the area of the shaded area is:

As = 12 - 6.28

As = 5.72

By dividing the area of the shaded area by the area of the rectangle we get the probability like this:

`P=(5.72)/(12)=0.48`

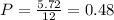
Then, the probability that a randomly chosen point lies in the shaded region is 0.48 (48%)