Let x be the number of sodas sold
Lef y be the number of hot dogs sold
At a baseball game, a vender sold a combined total of 208 sodas and hot dogs:
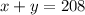
The number of hot dogs sold was 42 less than the number of sodas sold:
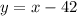
Use the next system of equations to solve the question:
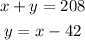
1- Use the second equation in the frist equation:

2- Solve x.
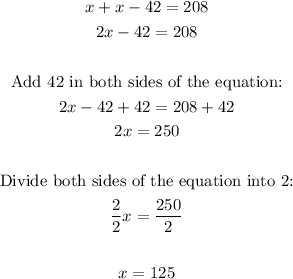
3- Use the value of x to solve y:
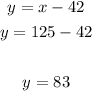
Then, the number of sodas sold was 125 and the number of hot dogs sold was 83