Question

How far above the ground is the dog's paw? Express your answer to the nearest inch.✓Submit30

Answer 1

We have a right triangle whose lengths are 26 inches and 36 inches.

We have that the largest side of a right triangle is the hypotenuse (c), and we can call the other side (one of the legs of the triangle) b. Then, using the Pythagorean Theorem, we have:

c = 36 inches.

b = 26 inches.

`c^2=a^2+b^2`

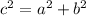
We can solve this equation for a^2, subtracting b^2 to both sides of the equation:

`c^2-b^2=a^2+b^2-b^2\Rightarrow c^2-b^2=a^2+0\Rightarrow a^2=c^2-b^2`

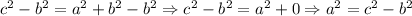
Then, we have:

`a^2=36^2-26^2\Rightarrow\sqrt[]{a^2}=\sqrt[]{1296-676}\Rightarrow a=\sqrt[]{620}\Rightarrow a=24.899799`

Rounding this value to the nearest inch, we have that the value for a = 25 inches.