Question

Hi, can you please help me with parts B and C? I need verification for my solutions, thanks!

Answer 1

a) constant of variation is 129.6

b) E = 129.6/d^2

c)

Step-by-step explanation:

Illumination, E varies inversely as distance squared, d²

Writing this mathemeatically:

`\begin{gathered} E\text{ }\alpha\text{ }(1)/(d^2) \\ E\text{ = k}(1)/(d^2)\text{ (to equate, we will introduce a constant)} \\ E\text{ = }(k)/(d^2) \\ \text{where k = cosntant of proportion /variation} \end{gathered}`

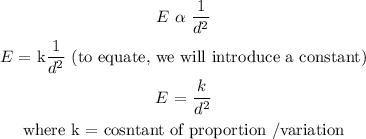
To get k, we will substitute for E and d in the equation

when E = 29.388 lux, d = 2.1 m

`\begin{gathered} E\text{ = }(k)/(d^2) \\ 29.388\text{ = }(k)/(2.1^2) \\ k\text{ = }29.388(2.1^2) \\ k\text{ = 129.60} \\ \text{Hence, constant of varaition is 129.60} \end{gathered}`

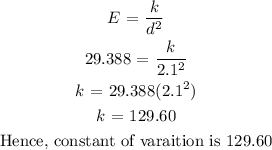
b) To get the equation that models this situation, we will substitute for k in the equation showing relationship between illumination (E) and distance (d)

`\begin{gathered} E\text{ = }(k)/(d^2) \\ E\text{ = }(129.6)/(d^2) \end{gathered}`

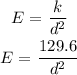
c) we need to find the distance when the illumination is 4.614 lux

Using the equation that models the situation:

`\begin{gathered} E\text{ = }(129.6)/(d^2) \\ 4.614\text{ = }(129.6)/(d^2) \\ 4.614(d^2)\text{ = 129.6} \\ d^2\text{ = }(129.6)/(4.614)\text{ = 28.0884} \\ d\text{ = }\sqrt[]{\text{28.0884}} \\ d\text{ = 5.2998} \\ To\text{ the nearest tenth, the distance is 5.3 meters} \end{gathered}`