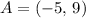Question

Find the coordinates of A if M(-1, 2) is the midpoint of AB and B has coordinates of (3,-5).

Answer 1

Hello there. To solve this question, we have to remember how to determine the coordinates of a point given the midpoint of a segment.

Given that M is the midpoint of the segment AB

`M=(-1,\,2)`

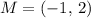
and that the point B has coordinates

`B=(3,\,-5)`

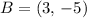
First, remember the formula for the distance between two points (x0, y0) and (x1, y1):

`d((x_0,\,y_0),\,(x_1,\,y_1))=√((x_0-x_1)^2+(y_0-y_1)^2)`

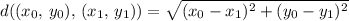
So that we know that the midpoint of a segment has the same distance from its ends.

In this case, we determine first the distance between the points M and B:

`\begin{gathered} d(M,\,B)=√((-1-3)^2+(2-(-5))^2)=√((-4)^2+7^2) \\ \\ \Rightarrow d(M,\,B)=√(16+49)=√(65) \\ \end{gathered}`

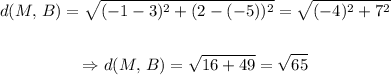
Next step, remember the formula for the midpoint of a segment

If A and B are the endpoints of the segment AB and has coordinates

`A=(x_A,\,y_A)\text{ and }B=(x_B,\,y_B)`

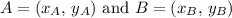
Its midpoint is given by

`M=\left((x_A+x_B)/(2),\,(y_A+y_B)/(2)\right)`

Such that we find

`M=(-1,\,2)=\left((x_A+3)/(2),\,(y_A-5)/(2)\right)`

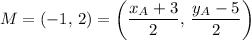
Hence we find that

`\begin{gathered} (x_A+3)/(2)=-1\Rightarrow x_A=-5 \\ \\ (y_A-5)/(2)=2\Rightarrow y_A=9 \end{gathered}`

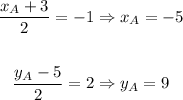
So the coordinates of the point A are

`A=(-5,\,9)`