Question

Solve ln(3x+4)−3ln(3)=ln(2x+1). Round answers to nearest hundredth.

Answer 1

`\ln (3x+4)-3\ln (3)=\ln (2x+1)`

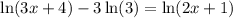
We can operate on that expression as shown below

`\begin{gathered} \ln (3x+4)-3\ln (3)=\ln (2x+1) \\ \Rightarrow\ln (3x+4)-\ln (3^3)=\ln (2x+1);\ln (z^y)=y\cdot\ln (z) \\ \Rightarrow\ln ((3x-4)/(3^3))=\ln (2x+1);\ln ((z)/(y))=\ln (z)-\ln (y) \end{gathered}`

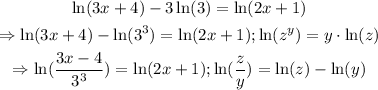
Remember that the function 'ln' is injective.This means that,

`\ln (z)=\ln (y)\Rightarrow z=y;y,z\in(0,\infty)`

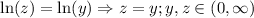
So,

`\begin{gathered} \ln ((3x-4)/(3^3))=\ln (2x+1) \\ \Rightarrow(3x-4)/(3^3)=2x+1 \\ \Rightarrow(3x-4)/(27)=2x+1 \end{gathered}`

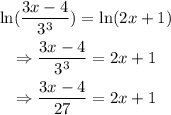
And this is simply a usual equation with one unknown. Solving for x,

`\begin{gathered} (3x-4)/(27)=2x+1 \\ \Rightarrow2x-(1)/(9)x=(4)/(27)-1 \\ \Rightarrow(17)/(9)x=-(23)/(27) \\ \Rightarrow x=-(23)/(51) \end{gathered}`

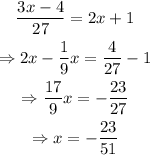
Now, we need to round to the nearest hundredth

`\begin{gathered} x=-(23)/(51)=-0.4209\ldots \\ x\approx-0.45 \end{gathered}`

Thus, the answer is x=-0.45 once we have rounded it