Question

in the graph shown below, are lines L1 and L2 perpendicular? explain. choose the correct statement below A) no,the lines L1 and L2 are not perpendicular because the product of their slopes does not equal -1B)no, the lines L1 and L2 are not perpendicular because the products of their slope equals -1C) yes, the lines L1 and L2 are perpendicular because the products of their slope equals -1D)yes, the lines L1 and L2 are perpendicular because the product of their slope do not equal -1

Answer 1

In order to see if the lines are perpendicular, we must compute their slopes.

The slope formula for two points (x1,y1) and (x2,y2) is given by

`m=(y_2-y_1)/(x_2-x_1)`

For instance, if we take these points in the line L1

`\begin{gathered} (x_1,y_1)=(-1,1) \\ (x_2,y_2)=(5,-2) \end{gathered}`

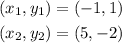
and substitute their values into the slope formula, we obtain

`\begin{gathered} m=(-2-1)/(5-(-1)) \\ m=(-3)/(5+1) \\ m=(-3)/(6) \\ m=-(1)/(2) \end{gathered}`

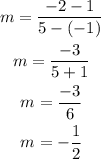
Similarly, we must do the same for line L2. If we take these points in the line L2

`\begin{gathered} (x_1,y_1)=(1,-4) \\ (x_2,y_2)=(7,5) \end{gathered}`

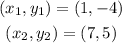
and substitute their values into the slope formula, we have

`\begin{gathered} M=(5-(-4))/(7-1) \\ M=(5+4)/(6) \\ M=(9)/(6) \\ M=(3)/(2) \end{gathered}`

Now, the perpendicular slope is the opposite reciprocal of the line to which it is perpendicular, that is

`M=-(1)/(m)`

must be fulfiled. Lets see if this occurs:

`\begin{gathered} M=-(1)/(-(1)/(2)) \\ M=(1)/((1)/(2)) \\ M=2 \end{gathered}`

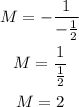
and we can see that 2 is not equal to 3/2. This imply that lines L1 and L2 are not perpendicular