The slope intercept form of the equation of a line is given as:
y = mx + c
where m = the slope of the line
c = the y - intercept of the line
1) Two line are parallel if they have the same slope
That is:

2) Two equations are perpendicular if the slope of one is the negative inverse of the other.
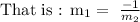
3) Two equations are coincidental if they have the same slope and the same y intercept
