Question

The function f(x) = x² - 6x+9 is shifted 5 units to the right to create g(x).What is g(x)?A. g(x) = (x - 5)^2 - 6(x - 5) +9B. g(x) = (x + 5)² - 6(x+5) +9C. g(x) = (x² - 6x +9) - 5D. g(x) = (x² - 6x + 9) + 5

Answer 1

Given the function:

`f(x)=x^2-6x+9`

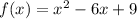
To create g(x), the function f(x) is shifted 5 units to the right.

Firstly, the graph of f(x) is shown below:

To create g(x), we have

The graph g(x) is shown below:

Hence, the g(x) function is expressed as

`g(x)=(x-5)^2-6(x-5)+9`

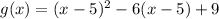
The correct option is A