The triangle in the question is a right triangle.
Recall that a right triangle that has an angle measuring 45 degrees is an isosceles triangle. This means that the two lines adjacent to the right angle are equal.
Going by this definition, we have that:
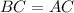
Therefore:
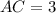
The length of the hypotenuse can be gotten using the Pythagorean Theorem:

Hence, we can calculate the value of the ratios provided:
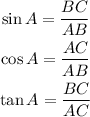
Using the calculated value, we have the answers to be:

ANSWER
