Question

Find an equation of the tangent line at the indicated point on the graph of the function.w = g(z) = 1 + square root of (6 - z), (z, w) = (5, 2)w = - (1/2)z + (9/2)w = (1/2)z - (9/2)w = (1/2)z + (9/2)w = - (1/2)z - (9/2)

Answer 1

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Write the given details

`\begin{gathered} w=g(z)=1+√(6-z) \\ (z,w)=(5,2) \end{gathered}`

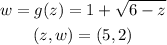
STEP 2: Explain Tangent line

Tangent Lines:

The tangent line to a function f(x) is a line that touches the graph of the function at one specific point of tangency where it has the same slope as the function at that point.

If x = a is the point of tangency, the tangent line can be written in slope-intercept form as:

`\begin{gathered} y=mx+b \\ where\text{ }m=f^(\prime)(a)\text{ }and\text{ }y|_(x=a)=f(a) \end{gathered}`

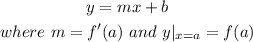
STEP 3: Find the tangent

We can first determine the slope of the tangent line by differentiating the function. Writing the function as:

`g(z)=1+(6-z)^{(1)/(2)}`

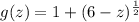
We find the derivative using the chain rule:

`\begin{gathered} \mathrm{Apply\:the\:Sum/Difference\:Rule}:\quad \left(f\pm g\right)'=f\:'\pm g' \\ =(d)/(dz)\left(1\right)+(d)/(dz)\left(\left(6-z\right)^{(1)/(2)}\right) \\ (d)/(dz)\left(1\right)=0,(d)/(dz)\left(\left(6-z\right)^{(1)/(2)}\right)=-\frac{1}{2\left(6-z\right)^{(1)/(2)}} \\ \\ =0-\frac{1}{2\left(6-z\right)^{(1)/(2)}} \\ =-\frac{1}{2\left(-z+6\right)^{(1)/(2)}} \\ \\ =-(1)/(2)(6-z)^{-(1)/(2)} \end{gathered}`

At the point of tangency, the slope is

`\begin{gathered} g^(\prime)(5)=-(1)/(2)(6-5)^{-(1)/(2)} \\ g^(\prime)(5)=-(1)/(2) \end{gathered}`

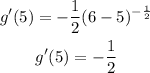
We can begin to write the equation of the tangent line in slope-intercept form

`w=-(1)/(2)z+b`

Substituting both coordinates of the point of tangency allows us to solve for the intercept:

`\begin{gathered} 2=-(1)/(2)(5)+b \\ -(1)/(2)\left(5\right)+b=2 \\ -(1)/(2)\cdot \:5+b=2 \\ -(5)/(2)+b=2 \\ (5)/(2)+b+(5)/(2)=2+(5)/(2) \\ b=(9)/(2) \end{gathered}`

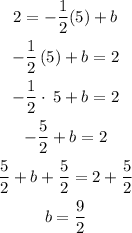
The complete equation of the tangent line at (5,2) is then

`w=-(1)/(2)z+((9)/(2))`