ANSWER
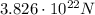
Step-by-step explanation
To find the gravitational force between them, apply the formula for gravitational force:
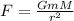
where G = gravitational constant = 6.6743 * 10^(-11) Nm²/kg²
m = mass of Saturn
M = mass of the sun
r = distance between them (radius of Saturn's orbit)
Therefore, the gravitational force between them is:
