To obtain the total volume of ice cream, the following steps are necessary:
Step 1: Make a sketch of the shapes stated in the question, as below:
Step 2: Recall the formulas for the volume of a cone and that of a hemisphere, as follows:
The volume of a cone is:
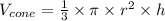
And, the volume of a hemisphere is:
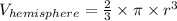
where, in both cases:
r = radius
h = perpendicular height
Step 3: Interpret the question to find clues, as follows:
"...that a half-scoop of ice cream is the shape of a hemisphere..." means that:
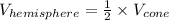
Thus, we have:
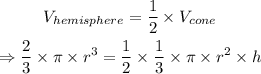
Since, the height of the cone is given to be 12 cm, we have:
![\begin{gathered} \Rightarrow(2)/(3)*\pi* r^3=(1)/(2)*(1)/(3)*\pi* r^2* h \\ \Rightarrow(2)/(3)*\pi* r^3=(1)/(6)*\pi* r^2* h \\ \text{Divide both sides by: }(2)/(3)*\pi* r^2 \\ \text{Thus:} \\ \Rightarrow\frac{(2)/(3)*\pi* r^3}{\text{ }(2)/(3)*\pi* r^2}=\frac{(1)/(6)*\pi* r^2* h}{\text{ }(2)/(3)*\pi* r^2} \\ \Rightarrow r=(1)/(4)* h \\ \sin ce\text{ h=12} \\ \Rightarrow r=(1)/(4)*12=(12)/(4) \\ \Rightarrow r=3\operatorname{cm} \end{gathered}]()
Step 4: Now that we have used the clue to find the radius of the hemisphere (and cone), we can now proceed to find the total volume of the figure, as follows:
Thus:
Since:
h = 12 cm
r = 3cm
and pie = 3.14 (as given), we have that:
![\begin{gathered} \Rightarrow\text{Total volume of ice cream = }_{}(1)/(3)*\pi* r^2(2r+h) \\ \Rightarrow\text{Total volume of ice cream = }_{}(1)/(3)*3.14*(3)^2(2(3)+12) \\ \Rightarrow\text{Total volume of ice cream = }_{}(1)/(3)*3.14*9(6+12) \\ \Rightarrow\text{Total volume of ice cream = }_{}(1)/(3)*3.14*9*^{}(18) \\ \Rightarrow\text{Total volume of ice cream = }_{}(508.68)/(3)=169.56 \\ \Rightarrow\text{Total volume of ice cream = }_{}169.6\operatorname{cm}^3\text{ (to the nearest tenth)} \end{gathered}]()
Therefore, the total volume of ice cream is 169.6 cubic centimeter