Question

At the beginning of an experiment, a scientist has 276 grams of radioactive goo. After 255 minutes, her sample has decayed to 17.25 grams.

Answer 1

`\begin{gathered} a)t1\text{/2}=63.75\min \\ b)G(t)=276\cdot((1)/(2))^{(t)/(63.75)} \\ c)131.65g \end{gathered}`

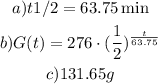
Step-by-step explanation

a) At the start of the experiment, the scientist had 276 grams of radioactive goo and after 255 minutes, the sample decayed to 17.25 grams.

To find the half-life, we can apply the formula for half-life:

`N(t)=N_0((1)/(2))^{\frac{t}{t1\text{/2}}_{}}`

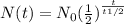
where N0 = initial amount

N(t) = amount after time t

t = time elapsed

t1/2 =half-life

From the question, we have that:

`\begin{gathered} N(t)=17.25g \\ N_0=276g \\ t=255\text{ mins} \end{gathered}`

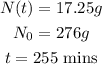
We have to find the half-life, t¹/₂. That is:

`\begin{gathered} 17.25=276((1)/(2))^{\frac{255}{t1\text{/2}}} \\ \Rightarrow(17.25)/(276)=((1)/(2))^{\frac{255}{t1\text{/2}}} \\ \Rightarrow0.0625=((1)/(2))^{\frac{255}{t1\text{/2}}} \end{gathered}`

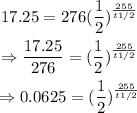
Converting to logarithmic function:

`\begin{gathered} \Rightarrow\log _{((1)/(2))}0.0625=\frac{255}{t1\text{/2}} \\ \frac{255}{t1\text{/2}}=(\log _(10)0.0625)/(\log _(10)0.5) \\ \frac{255}{t1\text{/2}}=4 \\ \Rightarrow t1\text{/2=}(255)/(4) \\ t1\text{/2=63.75 mins} \end{gathered}`

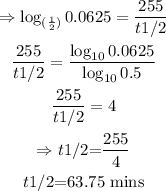
Therefore, the half-life is 63.75mins.

b) Therefore, using the half-life, we have that the equation G(t) for the amount of goo remaining at time t is:

`G(t)=276\cdot((1)/(2))^{(t)/(63.75)}`

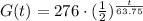
c) To find the amount of goo remaining after 68 mins, we have to find G(t) when t = 68.

That is:

`\begin{gathered} G(t)=276\cdot((1)/(2))^{(68)/(63.75)} \\ G(t)=276\cdot((1)/(2))^(1.067) \\ G(t)=276\cdot0.477 \\ G(t)=131.65g \end{gathered}`

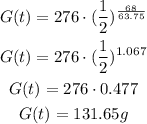
That is the amount remaining after 68 minutes.