Answer:
Option A is correct
Area of the unshaded region = 18(2√3 - π)
Explanations:
Note that triangle ABC is an equilateral triangle, therefore the area of triangle ABC will be found using the formula for the area of an equilateral triangle
![\text{Area of triangle ABC = }\frac{\sqrt[]{3}}{4}a^2](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/t1vihqn7t19u40il9u55.png)
where a represents each side of the triangle.
In triangle ABC , a = 6 + 6
a = 12 cm
![\begin{gathered} \text{Area of triangle ABC = }\frac{\sqrt[]{3}}{4}(12^2) \\ \text{Area of triangle ABC = }\frac{144\sqrt[]{3}}{4} \\ \text{Area of triangle ABC = }36\sqrt[]{3} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/o3g9etn3t4xwwfqbyzyk.png)
There are three sectors contained in the triangle, and each of them form an angle 60° with the center.
The radius, r = 6 cm
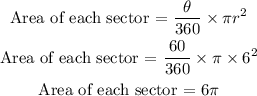
Area of the three sectors contained in the triangle = 3(6π)
Area of the three sectors contained in the triangle = 18π
Area of the unshaded region = (Area of the triangle ABC) - (Total Area of the sectors)
Area of the unshaded region = 36√3 - 18π
Area of the unshaded region = 18(2√3 - π)