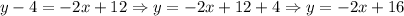Question

Find the equation of the line that is parallel to the line 4x+2y=24 that goes through the point (6,4)

Answer 1

We have that the linear equation is:

4x + 2y = 24

We need to convert this standard form of the line equation into the slope-intercept form of the line equation, that is, y = mx + b. Then, we can do as follows:

1. Subtract 4x from both sides of the equation:

`4x-4x+2y=24-4x\Rightarrow2y=-4x+24`

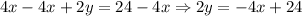
2. Divide both sides of the equation by 2 (to isolate y):

`(2y)/(2)=-(4)/(2)x+(24)/(2)\Rightarrow y=-2x+12`

Now, we have the slope-intercept form of the line equation. The slope, m, is m = -2.

Since we need to find a parallel line to this line, the new line needs to have the same slope, that is, m = -2.

Then, we have the slope, m = -2, and the point (6, 4). We can use the point-slope form of the line equation to find the parallel line. Therefore, we have:

`y-y_1=m(x-x_1)\Rightarrow y-4=-2(x-6)`

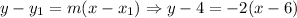
And then, expanding this equation, we finally have that the parallel line is:

`y-4=-2x+12\Rightarrow y=-2x+12+4\Rightarrow y=-2x+16`