Question

HELPPPPPPPPPPP PLEASEEEEEE!!!!!

Tyler is 6 feet tall. when he puts the mirror on the ground 20 feet from the base of peak A. and stands 3 feet back from the mirror he can see the peak.
1. According to the information given what canyou determine about the triangles formed by tyler The mirror and the peak? How do you know the relation ship between the two triangles?

2. to find the height of the peak. List the corresponding sides and angles of the two triangles.

3. What is the height of the peak?

Answer 1

I hope this helps you

Answer 2

Explanation:

In the figure attached, A is the peak of mountain AB, ED is Tyler who is 6 feet high.

Mirror placed at C, is 20 feet from the base of peak. Tyler is 3 feet away from the mirror.

1). When Tyler sees the peak in the mirror, angle of incidence " i " and angle of reflection " r " made by incident ray AC and reflected ray EC will be equal.

Now we can easily say ∠ r = ∠ E ( Alternate angles )

∠ i = ∠ A ( alternate angles)

Since ∠ i = ∠ r

Therefore, ∠ A = ∠ E

∠B = ∠D = 90°

and ∠ACB = ∠ECD

Hence ΔABC is similar to ΔCDE.

2). Corresponding sides of these similar triangles are AB and ED, BC and CD, AC and CE.

3). tanE =
`(CD)/(DE)=(3)/(6)`

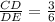
tanE = 0.5

∠ E =
`tan^(-1)(0.5)=26.57` degrees

Now ∠E = ∠A = 26.57°

Therefore, tan(26.57) =
`(20)/(AB)`

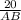
0.5 =
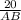
`(20)/(AB)`

AB =
`(20)/(0.5)=40`

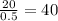
Therefore, height of the peak AB is 40 feet.