Question

It is 1.9 miles from a house to a restaurant and 1.2miles to a pier, as shown at the right. The anglebetween the two lines of sight is 87°. How far is it fromthe pier across the water to the restaurant.

Answer 1

Since two side sides of the triangle and an angle is known, we apply the Cosine rule

Formula for Cosine rule is given below,

Where a is distance between the house and pier,

b is the distance between the house and restaurant,

c is the distance between the pier and the restaurant,

C is the angle opposite c

`c^2=a^2+b^2-2ab\cos C`
`\begin{gathered} \text{Where,} \\ a=1.2\text{ miles} \\ b=1.9\text{ miles and } \\ c=unknown^{} \\ C=87^0 \end{gathered}`

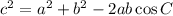
Substituting the variables into the given formula above,

`\begin{gathered} c^2=a^2+b^2-2ab\cos C \\ c^2=(1.2)^2+(1.9)^2-2(1.2)(1.9)\cos 87^0 \\ c^2=1.44+3.61-4.56(0.05234) \\ c^2=5.05-0.2387 \\ c^2=4.8113 \\ \sqrt[]{c^2}=\sqrt[]{4.8113} \\ c=2.1935\text{ miles} \\ c\approx2.19\text{ miles} \end{gathered}`

Hence, the distance from the pier to the restaurant is 2.19 miles.