Given:
In 1995, the population is 7800.
In 1997 population is 8300.
it implies that population is increase by 500 after 2 years.
As ,the population continues to change linearly.
From 1987 to 1995 there are 8 years and from 1987 to 1997 10 years.
Note: here the x values are from the year 1987 and y values are population.
We have two points ( 8,7800) and (10,8300)
Slope of the equation is given by,
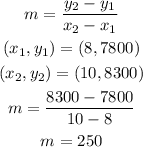
The slope -point form of equation of line is,
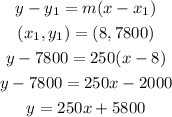
An equation for the moose population P as a function of t years since 1987 is,
P(t)=250t+5800.
The population in the year 2003 is,
Note: we need to determine the years from 1987 to 2003
2003-1987=16
So, the population in the year 2003 that means after 16 years from 1987.

Answer:
1) An equation for the moose population P as a function of t years since 1987 is,
P(t)=250(t)+5800.
2) The population in the year 2003 is 9800.