Question

1.A mass of 15.50 kg comes into contact with a force of 2655 N, directed North, for 0.05 seconds. After this contact, the object obtains a velocity of 45.00 m/s [N45W]. Determine the initial velocity of the object.

Answer 1

In order to calculate the initial velocity, first let's calculate the acceleration generated by this force, using the second law of Newton:

`\begin{gathered} F=m\cdot a\\ \\ 2655=15.5\cdot a\\ \\ a=(2655)/(15.5)=171.29\text{ m/s} \end{gathered}`

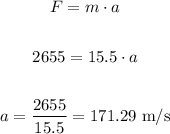
Let's calculate the change in velocity caused by this acceleration in 0.05 seconds:

`\Delta V=a\cdot t=171.29\cdot0.05=8.56\text{ m/s}`

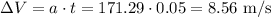
Now, let's draw a diagram to understand the velocity vectors:

Let's calculate the vertical and horizontal components of the final velocity:

The horizontal component of the final velocity is equal to the initial horizontal velocity:

`V_(ix)=V_x=-31.82\text{ m/s}`

The vertical component of the final velocity is equal to the sum of the initial vertical velocity and the velocity added by the acceleration:

`\begin{gathered} V_y=V_(iy)+\Delta V\\ \\ V_(iy)=V_y-\Delta V=31.82-8.56=23.26\text{ m/s} \end{gathered}`

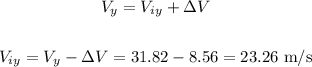
Now, we can calculate the initial velocity using the Pythagorean theorem:

`\begin{gathered} V_i^2=V_(ix)^2+V_(iy)^2\\ \\ V_i^2=(-31.82)^2+23.26^2\\ \\ V_i^2=1012.51+541.03\\ \\ V_i^2=1553.54\\ \\ V_i=39.41\text{ m/s} \end{gathered}`

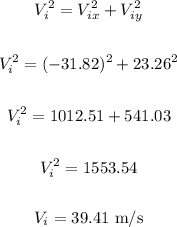
To calculate the direction, we can do the following:

`\begin{gathered} \theta=\tan^(-1)((V_(iy))/(V_(ix)))\\ \\ \theta=\tan^(-1)((23.26)/(-31.82))\\ \\ \theta=\tan^(-1)(-0.73099)\\ \\ \theta=143.83° \end{gathered}`

So the direction is N 53.83 W.