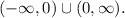Question

Determine the range of y=2/(2x+1)

Answer 1

To solve this question we will solve the given equation for y and we will analyze the possible values of y (that will be the range of the given function).

Assuming that 2x+1≠0, and multiplying the given equation by 2x+1 we get:

`\begin{gathered} y\cdot(2x+1)=(2)/(2x+1)\cdot(2x+1), \\ 2yx+y=2. \end{gathered}`

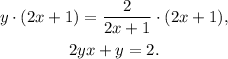
Subtracting y from the above equation we get:

`\begin{gathered} 2yx+y-y=2-y, \\ 2yx=2-y\text{.} \end{gathered}`

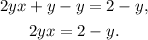
Dividing the above equation by 2y we get:

`\begin{gathered} (2yx)/(2y)=(2-y)/(2y), \\ x=(2-y)/(2y) \end{gathered}`

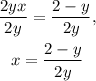
Therefore, y can be all real numbers except zero.

Answer:

`(-\infty,0)\cup(0,\infty)\text{.}`