Question

Suppose the triangles shown are similar with angle A = angle D, angle B = angle E, and angle C = angle F. Answer the question.

Answer 1

Similar triangles have the same ratio between corresponding sides:

`(AB)/(DE)=(BC)/(EF)=(CA)/(FD)`

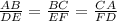
We have the sizes of the sides:

• AB = 17

,

• BC = 22

,

• CA = 2x-7

,

• DE = 34

,

• EF = 44

,

• FD = 2x+4

We use the ratio property to find x:

`\begin{gathered} (BC)/(EF)=(CA)/(FD) \\ (22)/(44)=(2x-7)/(2x+4) \\ (1)/(2)=(2x-7)/(2x+4) \end{gathered}`

And now we clear x:

`\begin{gathered} (1)/(2)=(2x-7)/(2x+4) \\ 2x+4=2(2x-7) \\ 2x+4=4x-14 \\ x(2-4)=-14-4 \\ x=(-14-4)/(2-4)=(-18)/(-2)=9 \end{gathered}`

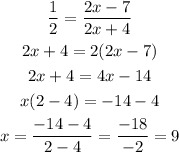
Now that we have x = 9, we can find the lenght of side DF (DF and FD are the same side):

`FD=2x+4=2\cdot9+4=18+4=22`

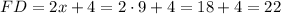
The answer is option C, FD = 22