Given:
A.)
Slope of the line (m) = -2/3
Y-intercept (b) = 3
The given can be used to make an equation under the Slope-Intercept Form:
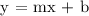
By substituting m and b to y = mx + b, we can generate the equation.
We get,
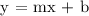
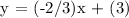
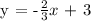

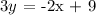
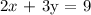
Therefore, the equation match to m = -2/3 and b = 3 is 2x + 3y = 9.
B.)
Slope of the line (m) = -3/2
x,y = 4,-1
To be able to generate the equation, let's first determine the y-intercept (b). We can get it by substituting m = -3/2 and x,y = 4,-1 to the equation y = mx + b.
We get,
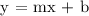
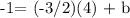
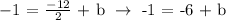

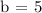
Since we now found that the y-intercept (b) = 5, let's substitute b and m = -3/2 to y = mx + b to generate the equation.
We get,
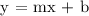
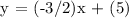
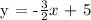
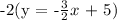
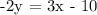
Therefore, the equation that match m = -3/2 and (4,-1) is -2y = 3x - 10.