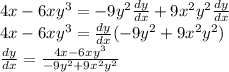Question

Implicit differentiation in terms of x and y

Answer 1

For implicit differentiation, you are using the chain rule

`f'(x) = g'(u(x))* (du)/(dx)`
Except u(x) = y, So after every "y" term is differentiated it will be multiplied by dy/dx.

17)
`y^3 +4 = 3x \\ 3y^2 (dy)/(dx) +0 = 3`
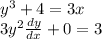
Then you solve for dy/dx as if its a variable.

`(dy)/(dx) = (3)/(3y^2) = (1)/(y^2)`

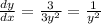
18) Here lets review product rule:

`(fg)' = f'g + fg'`
Take derivative of each term

`2x^2 = -3y^3 +3x^2y^3 \\ 4x = -9y^2 (dy)/(dx) + (6x)(y^3) + (3x^2)(3y^2 (dy)/(dx)) \\ 4x = -9y^2 (dy)/(dx) +6xy^3 +9x^2y^2 (dy)/(dx)`
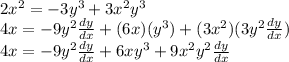
Solve for dy/dx using factoring:

`4x - 6xy^3 = -9y^2 (dy)/(dx)+9x^2 y^2 (dy)/(dx) \\ 4x - 6xy^3 = (dy)/(dx)(-9y^2 +9x^2 y^2) \\ (dy)/(dx) = (4x - 6xy^3)/(-9y^2 +9x^2 y^2)`