a)
From the graph, the coefficient of a, b, and c are:
a = -15.19
b = -1.39
c = 5.24

b)
To find the height after 0.30 seconds, you will substitute t = 0.30

c)
To find the height after 0.52 seconds, you will substitute t = 0.52
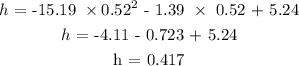
d)
0.30 seconds is more reliable.
e)
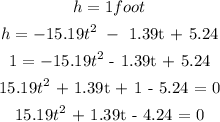
t = 0.48455
Final answer
t = 0.48 seconds