Given the two functions
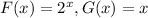
We are tasked to plot (F-G)(x).
The first step here is to get the resulting function (F-G)(x). We have
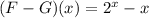
Now, we need to assign values of x and evaluate them at the function (F-G)(x) to get a value. We will get coordinate points and we will plot them at the cartesian coordinate plane. I will use values of x = [-3,3]. We get the following results
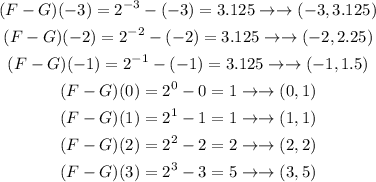
The plot is provided by the image below.