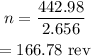Question

A car accelerates uniformly from rest andreaches a speed of 32.1 m/s in 13.8 s. Thediameter of a tire is 84.7 cm.Find the number of revolutions the tiremakes during this motion, assuming no slipping.Answer in units of rev.

Answer 1

Given that the speed is v = 32.1 m/s and time is t = 13.8 s.

Also, the diameter of the tire is d = 84.7 cm

We have to find the number of revolutions of the tire.

As the diameter is 84.7, so the radius will be

`\begin{gathered} r=(d)/(2) \\ =(84.7)/(2) \\ =0.423\text{ m} \end{gathered}`

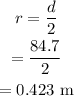
The circumference of the circle will be

`C=2\pi r`

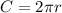
Substituting the values, the circumference will be

`\begin{gathered} C=2*3.14*0.423 \\ =2.656\text{ m} \end{gathered}`

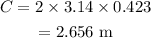
The distance can be calculated using speed and time,

`\begin{gathered} s=v* t \\ =32.1*13.8 \\ =442.98\text{ m} \end{gathered}`

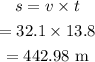
To find the number of revolutions, the formula will be

`n\text{ =}\frac{\text{total distance}}{circumference}`

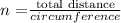
Substituting the values, n will be

`\begin{gathered} n=(442.98)/(2.656) \\ =166.78\text{ rev} \end{gathered}`