Solution
Question 6)
The price of the Penthouse is $2.4 million
Down Payment is $2.1 Million
So the amount that must be financed is $2.4 million - $2.1 million
= $0.3 million or $300,000
Question 7)
A mortgage is loan one takes to buy a house or other property. To determine the monthly loan payment (P) one uses the formula
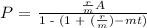
Where A is the loan amount, m is the number of payments per year, t is the number of years, and r is the interest rate of the loan.
To evaluate two mortgages in terms of economics it is advised to calculate the interest outgo on each of them and compare.
Monthly Payments (P) for the loan can be found using the formula

Where A is the loan amount, m is the number of payments per year, t is the number of years, and r is the interest rate.
For a 30-year loan at 8%:
Given data
A = $300,000
r = 8%
t = 30
m = 12
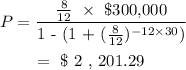
The monthly loan payment for a 30-year loan at 8% would be $2,201.29
Question 8)
For a 20-year loan at 7.5%:
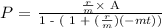
Given data
A = $300,000
r = 7.5%
t = 20
m = 12
Substitute the values in the equation.

The monthly loan payment for a 20-year loan at 7.5% = $2,416.78
Question 9)
30 years loan
Find the number of months in 30 years by multiplying 30 by 12
Number of months in 30 years = 30 x 12 = 360 months
Next, calculate the interest payment.
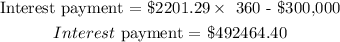
20 years loan
Find the number of months in 20 years by multiplying 20 by 12
Number of months in 20 years = 20 x 12 = 240 months
Next, calculate the interest payment.
![\begin{gathered} Interest\text{ payment = \$2416.78 }*\text{ 240 - \$300000} \\ Interest\text{payment=}\operatorname{\$}580,027.2\text{-}\operatorname{\$}\text{*300,000} \\ Interest\text{payment=}\operatorname{\$}280,027.20 \end{gathered}]()
20 years mortgage is more economical to choose because you will pay less interest.
Question 10)
To find the money saved in the interest, you will subtract the interest paid in 20 years from the interest paid in 30 years.
Interest saved = $492464.4 - $280027.2
Interest saved = $212,437.20